Miten löytää isosceles kolmion alue

Matematiikka ja erityisesti geometria, mukaankoululaisten kyselytutkimukset, yksi suosituimmista oppitunneista ja kaikki, koska ne antavat sinut opettelemaan lukuisia kaavoja, jotka elämässä 90% nykyisistä aikuisista eivät ole löytäneet käytännön sovellusta. Mutta hetkeksi opimme kaavoja, ratkaisemme ongelmia, emme anna yhtälöitä siitä, että ne voivat olla hyödyllisiä meille elämässä, vaan koska se kehittää ajattelua ja logiikkaa. Jopa muinaiset kreikkalaiset viisaat sanoivat, että ihmisen älyä voidaan mitata matemaattisten tieteiden tuntemuksella. Ja koska olet päättänyt tutustua kaavojen soveltamiseen isosceles kolmioon - otamme itsemme kädestä ja lue koko artikkeli.
Ennen kuin alat vastata kysymykseen, miten löytääisosceles-kolmion alueelle ja menemään artikkelin käytännön osaan, jossa kaavat ja laskelmat on annettu, tarkoittakaamme itse käsitystä. Isosceles kolmio on kolmio, jossa kaksi kolmesta sivusta on pituudeltaan samanlaisia, joita kutsutaan sivupuoliksi. Säännöllisen kolmion tapauksessa, jossa kaikki sivut ovat yhtä suuria, katsotaan myös isosceles, mutta päinvastoin, kun isosceles kolmio pidetään oikein - on väärä.
Kolmion sivut pitäisi nimetä. Teemme niin tällä tavalla, kuten alla olevassa kuvassa: a - sivut, b-pohja ja h-korkeus.
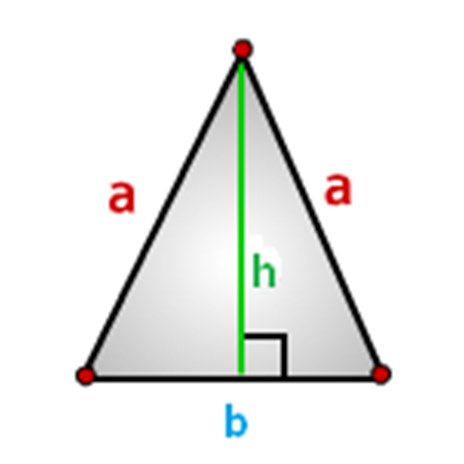
Kuinka laskea isosceles kolmion alue, kaavat.
Kun olemme tehneet merkintöjä korkeuden, sivu- ja kulma, voit alkaa ratkaista ongelman.
Aluksi selvitämme, mitä tiedämme.
Jos korkeus ja pohja - sitten klassinen kaava (* - kertolasku):
S = ½ * b * h
Korvataan esimerkiksi numeroita, joissa: h = 16, b = 18, saimme seuraavat:
S = ½ * 18 * 16 = 9 * 16 = 144;
Isosceles-kolmion pinta-ala on S = 144 cm2
On olemassa myös muita kaavoja, jotka auttavat meitäkuinka tietää isosceles kolmion alue. Yksi tällainen kaava on Heronin menetelmä. Älkäämme kirjoittako monimutkaista kaavaa, otamme pohjimmiltaan lyhennetyn:
S = ¼ b √4 * a2-b2
On selvää, että b on pohja ja - tasapuoliset puolet. Kaava soveltuu tilanteeseen, jossa h-korkeus on tuntematon.
Korvataan arvot, anna a = 6, b = 3, saamme seuraavaa:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Voit laskea alueen, joka vastaa kolmion sivuja ja sivujen välistä kulmaa:
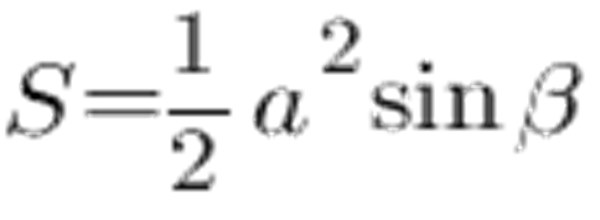
Sine-taulukon mukaan kulma 45 °: ssa on 0,7071, puoli a ja annetaan sen olla 6 cm, saimme seuraavat:
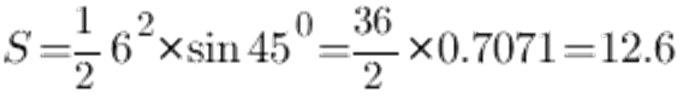
Tämän seurauksena isosceles-kolmion pinta-ala on 12,6 cm2.
On myös mahdollista laskea alue, mukaan lukienmukaan lukien isosceles kolmio, mutta ne ovat melko monimutkaisia eivätkä koske "elementaarisia" laskelmia, kuten yllä annettuja, monimutkaisen matematiikan käsitteessä. Ja ei kannata puhua asioista, joita myös opettajat, joilla on kokemusta, eivät ymmärrä.
Joten, voit hengittää huokauksen helpotusta, tässäpienen geometrian suunnan etsittäessä isosceles-kolmiota, katsotaan olevan täydellinen, ja artikkelin lukemisen tuloksena saatu tieto on "viisi".














